Surface tension. Weight and volume of the drop of liquid
This online calculator calculates the weight and the volume of the drop given the surface tension, diameter of the capillary tube, and density of the liquid
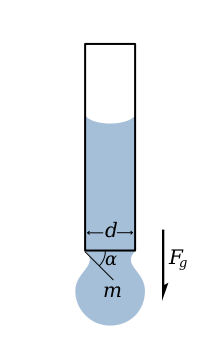
The picture on the left depicts a drop of liquid that is suspended from the end of a tube by surface tension. This force is proportional to the length of the boundary between the liquid and the tube and is given by
,
where - surface tension coefficient, newtons per meter, N/m
Drop is suspended as long as the vertical component of the surface tension force is equal to the gravity force, that is
The maximum applied surface tension force, when alpha equals 90°, gives the maximum weight of a drop of liquid with given surface tension.
, thus
Having the mass and density of the liquid, the volume is trivial.
In reality, drop detaches where "neck" is formed, slightly below the end of the tube, so diameter used should be less than tube diameter. But, if high precision is not required, this is often neglected.
Also, in this calculator, I estimate the maximum diameter of the tube, which allows drops. I assume that for a drop to be formed, surface tension force should be capable of holding at least hemisphere. Thus, given the density of the liquid, the formula becomes
and the radius is,
A couple of notes on the calculator below. First, it does not calculate weight and the volume if tube diameter is more than given by the equation above. Second, the default values for density of liquid and surface tension coefficient are given for water.
Comments